Trading Squeeth vs Deribit

The strategy below trades Squeeth against an approximate replicating portfolio of Deribit options. For streches of time, Squeeth IV tends to be meaningfully higher than the relevant options IV. This provides an opportunity to short Squeeth, long options, construct a delta/gamma neutral portfolio, and earn theta via Squeeth’s funding rate.

Background

Squeeth Basics

Squeeth is a power perpetual that provides exposure to $\text{ETH}^2$. It works like a perpetual swap tracking the index $\text{ETH}^2$ and gives option-like exposure to convexity without strikes and expiries.

Compared to a 2x levered ETH, long Squeeth provides additional upside, protected downside, and no liquidations. This is similar to always holding an ATM call option. Since this position provides positive gamma, longs pay shorts a funding rate. Short Squeeth provides short $\text{ETH}^{2}$ exposure collateralized by ETH. This is similar to always selling an ATM straddle. Since this position provides negative gamma, shorts earn the funding rate paid by longs. It is possible for the funding rate to go negative, but Squeeth should generally trade at a premium to $\text{ETH}^{2}$ due to the convexity.

Squeeth positions are represented by the fungible ERC20 token, oSQTH, which is traded on Uniswap v3.

Long Squeeth

To long Squeeth, you swap ETH for oSQTH in the Uniswap pool. To close your position, simply swap back.

Short Squeeth

A short position is represented as a vault in Squeeth’s Controller contract. The steps are: put down ETH as collateral, mint oSQTH, and swap for ETH in Uniswap. To close your position, swap back for oSQTH tokens, burn them in the Controller contract, and unlock your collateral. You can also use Uniswap LP tokens as collateral; this is useful for capital efficient LPing, but irrelevant to this strategy.

Funding

Unlike standard perpetuals where longs make direct cash payments to shorts, Squeeth uses in-kind funding. There is a transfer of value from longs to shorts based on the relative price of the index and the traded price of oSQTH. As a long, the value of your oSQTH position declines relative to $\text{ETH}^2$. As a short, the value of your oSQTH debt adjusts down. Hence you can monetize earned funding by unlocking collateral from your vault and selling for USD stablecoin.

In the smart contracts, this mechanism is implemented via a global variable, the normalization factor, which represents the cumulative funding paid since the creation of Squeeth. It was initiated at 1. It is updated every time the contract is touched and so funding is paid out somewhat continuously. The steps are:

1. Compute current prices in USD terms, $\text{oSQTH}_{t}$ and $\text{ETH}_{t}$, from 420 second TWAPs of the oSQTH/ETH and ETH/USDC Uniswap v3 pool oracles
2. Update:

$\begin{aligned} \text{Squeeth}_{t} &= \frac{\text{oSQTH}_{t}}{\text{normalization\_factor}_{t}} \times 10000\\ \text{rFunding}_{t} &= \frac{\text{hours since last update}}{\text{420 hours}}\\ \text{multiplier}_{t} &= \left(\frac{\text{ETH}_{t}^{2}}{\text{Squeeth}_{t}}\right)^{\text{rFunding}_{t}}\\ \text{normalization\_factor}_{t + 1} &= \text{multiplier}_{t} \times \text{normalization\_factor}_{t} \end{aligned}$

The current funding rate is essentially the percent difference in the mark and index prices, but this funding is paid over a period of 420 hours or 17.5 days. Hence the formula for $\text{multiplier}_{t}$, a value which should be less than 1 given Squeeth’s convexity premium. Notice that if the normalization factor decreases by 1% and the price of ETH holds constant, the price $\text{oSQTH}_{t+1}$ decreases by 1% as well. This represents the 1% funding paid by longs to shorts. The 10,000 factor is included just to make units of oSQTH readable.

The plot below from the Opyn team shows a hypothetical scenario with constant funding from 11/2020 to 11/2021: 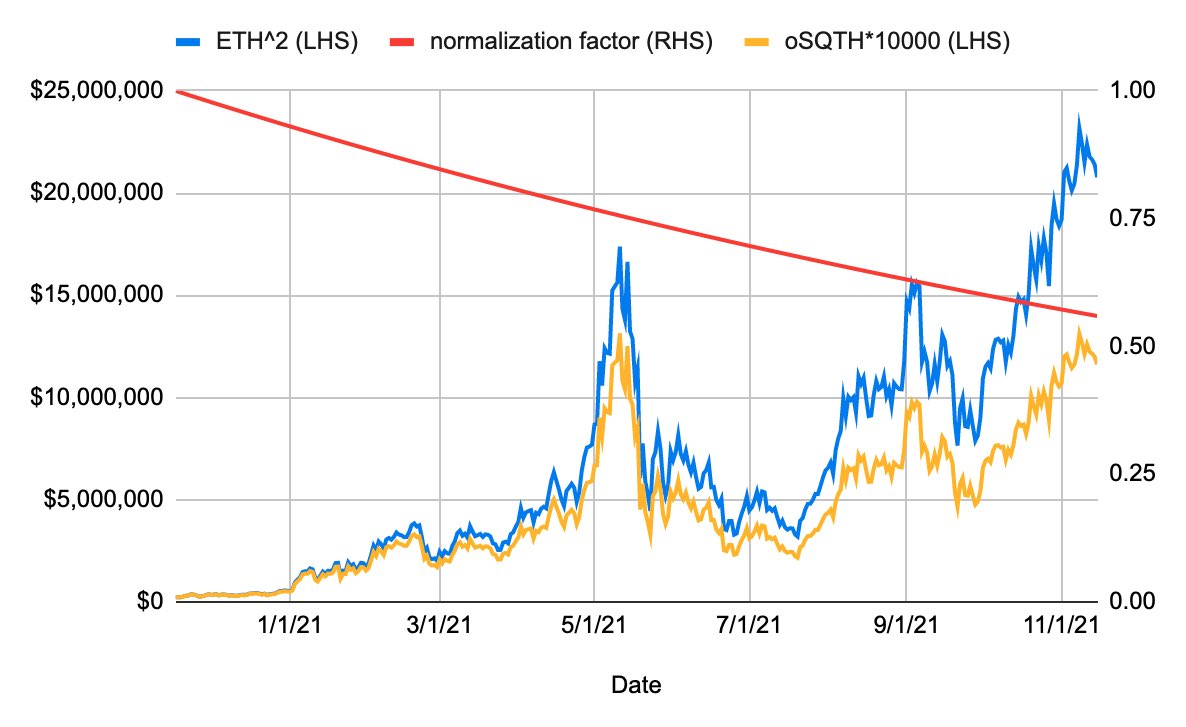We see the value of oSQTH $\times 10,000$ declines relative to $\text{ETH}^2$ over time and longs have paid shorts cumulative funding of around 50%.

Collateral and Liquidations

To open a short Squeeth position, you have to put down ETH collateral. If the value of the collateral falls below 1.5x the value of your oSQTH debt, you can be liquidated. The contracts compute: $\begin{aligned} \text{collateral\_ratio}_{t} &= \frac{\text{units of ETH collateral}}{\left(\text{units of oSQTH debt} \times \text{normalization\_factor}_{t} \times \text{ETH}_{t} \right) / 10,000} \end{aligned}$ There is a minimum collateral requirement of 6.9 ETH to ensure liquidator incentives in high gas environments.

Pricing

Below is a pricing model for Squeeth that can be used to trade it against Deribit options. The exact replicating portfolio for Squeeth is complex and impractical to trade. Check the last section.

Pricing a Power-2 Future

Instead of a power-2 perpetual, first consider a power-2 future which expires $\tau$ days from now. Let $S_{t}$ be the price of ETH on day ${t}$. Under Black-Scholes assumptions, fair value is: $D(t, \tau) = S_t^2 \exp\left(\frac{\tau}{365}{\left(r + \sigma^2\right)}\right)$ where $\sigma$ is the annualized vol and $r$ is the risk-free rate. The derivation is here. Now assume $r = 0$.

Pricing a Power-2 Perpetual

Consider a power-2 perpetual. Say the mark price for this instrument is $M_{t}$, it has a funding frequency of $N$, and a funding period of $P$ days. That means $N$ times over $P$ days, there is a funding payment made of value $\frac{M_{t} - S_t^2}{N}$. Using the no-arbitrage argument from the Everlasting Options paper fair value is: $D_{\infty}(t, P) = \frac{1}{N} \sum_{i=1}^{\infty} \left(\frac{N}{N + 1} \right)^{i} D(t, T_{i}) = S_t^2 \left(\frac{1}{(N + 1) \exp\left(-\frac{P \sigma^{2}}{365 N}\right) - N}\right)$ where $T_i = \frac{P}{N}i$ denotes the times of the future funding payments. We see the power-2 perpetual is an infinite weighted average of power-2 futures. The second equality assumes constant volatility and sums the resulting geometric series.

When $N$ is large relative to the carry, a power-2 perpetual is well approximated by a power-2 future with expiry $P$ days from now. One way to see this is that the weighted average of the future expiry times is $P$: $\lim_{N \rightarrow \infty} \frac{1}{N} \sum_{i=1}^{\infty} \left(\frac{N}{N + 1} \right)^{i} T_{i} = P$

Squeeth IV

For Squeeth, $P$ = 17.5 days and $N \rightarrow \infty$ since funding is supposed to be continuous. In practice, $N \approx 17.5 \times 24 \times 1 = 420$ since the normalization factor updates on average once an hour. Below we see for reasonable values of $\sigma$, Squeeth is well-approximated by a power-2 future with expiry in 17.5 days. Here $\text{Approx\_IV}(t, 17.5)$ was calculated by plugging in Squeeth prices into the IV formula for power-2 futures.

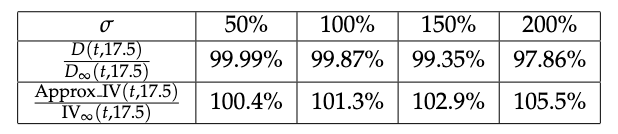
Hence we can say $\text{Squeeth}_{t} \approx D(t, 17.5)$ and extract the following IV: $\begin{aligned} \text{Squeeth\_IV}_{t} = \sqrt{\frac{365}{17.5}\times \ln\left(\frac{\text{Squeeth}_{t}}{S_{t}^2} \right)} \end{aligned}$

Squeeth Greeks

Let $p = \frac{17.5}{365}$. Under the approximation above, we get the following Greeks for Squeeth:

• Delta: $\Delta_{t} = 2S_{t}\exp\left(\sigma^{2}p\right)$
• Gamma: $\Gamma_{t} = 2\exp\left(\sigma^{2}p \right)$
• Vega: $\mathcal{V}_{t} = \frac{2\sigma p S_{t}^2 \exp\left(\sigma^{2}p\right)}{100}$
• Theta (daily): $\Theta_{t} = \frac{-\sigma^{2}S_{t}^2 \exp\left(\sigma^{2}p\right)}{365}$

To convert these into per oSQTH quantities, multiply by $\frac{\text{normalization\_factor}_{t}}{10,000}$.

Replicating Portfolio of a Power-2 Future

Consider a power-2 future expiring $\tau$ days from now. From Carr and Madan 2001, any payoff function of terminal price, $g(S_{T})$, can be replicated as follows: $g(S_{T}) = g(A) + g'(A)(S_{T} - A) + \int_0^A (K - S_{T})^+ g''(S_{T})dK + \int_A^\infty (S_{T}-K)^+ g''(S_{T})dK$ In our case, $g(S_{T}) = S_{T}^2$. We can set $A = K_0$, the strike cutoff closest to the current option-implied forward price, $F_t$. Then, we have: $S_{T}^2 = K_{0}^2 + 2K_{0}(S_{T} - K_{0}) + 2\int_0^{K_0} (K - S_{T})^+ dK + 2\int_{K_0}^\infty (S_{T}-K)^+ dK$ Hence the replicating portfolio is a zero coupon bond with face value $K_0^{2}$, $2K_{0}$ of the forward, and $2dK$ of OTM options across all strikes with expiry exactly $\tau$ days from now.

Replicating Portfolio IV

The replicating portfolio above seems to imply the Squeeth IV is a sort of average of 17.5-day option IVs across all possible strikes. Taking expectations of the last equation in a risk-neutral world, we get: $\mathbb{E}[S_{T}^2] = K_{0}^2 + 2K_{0}(F_t - K_{0}) + 2\int_0^{K_0} P_t(K) dK + 2\int_{K_0}^\infty C_t(K) dK$ where $P_t(K)$ and $C_t(K)$ are prices of OTM puts and calls across all strikes $K$. By setting $\mathbb{E}[S_{T}^2] = D(t, 17.5)$ and solving for $\sigma$, we get the following IV for the options replicating portfolio: $\text{Option\_IV}_{t} = \sqrt{\frac{365}{17.5} \times \ln\left(\frac{K_{0}^2 + 2K_{0}(F_t - K_{0}) + 2 \sum_{i} P_{t}(K_i) \Delta K_i + 2 \sum_{i} C_{t}(K_i) \Delta K_i }{S_t^{2}}\right)}$ Here the summations come from discretizing the integral. We can compute $F_{t}, K_0$ and $\Delta K_{i}$ from data on 17.5-day options with a methodology very similar to the VIX or DVOL.

Squeeth vs Option IVs

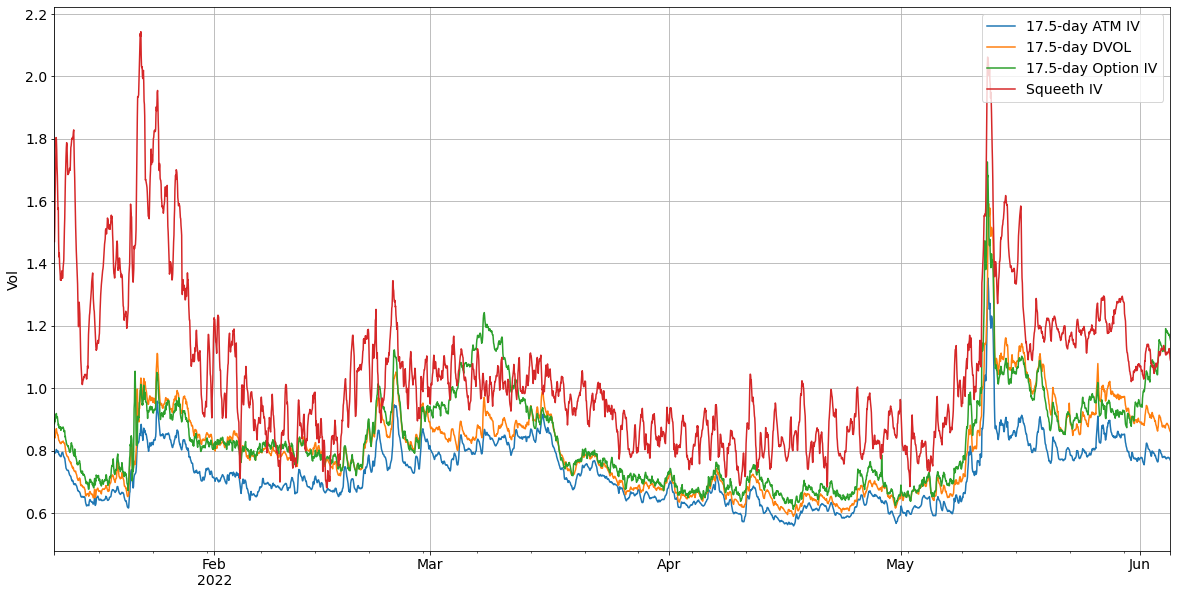
In simulations, we can verify $\text{Option\_IV}_{t} = \text{Squeeth\_IV}_{t}$ and replicating portfolio greeks match Squeeth greeks. In reality, Squeeth IVs (red) often tend to be higher than the replicating portfolio IVs (green). This creates a trading opportunity: short Squeeth and long options. We can keep the portfolio delta/gamma neutral and earn theta via Squeeth’s funding rate.

The Squeeth IVs here are computed from raw time series of oSQTH prices, ETH prices and the normalization factor. The option IVs are computed from top of the order book data from options on Deribit. All the analysis was done at the hourly frequency. As a benchmark, I also plot the 17.5-day ATM IV and DVOL.

Strategy

High-Level Description

The strategy works as follows:

• When the ratio of Squeeth to option IVs is large, go short $50K oSQTH and buy a strip of Deribit options with expiry close to 17.5 days. Size the options position to neutralize the negative gamma from short oSQTH.
• Manage ETH collateral in the Squeeth vault keeping the ratio close to 2. This approximately neutralizes the negative delta from the short oSQTH.
• Manage an ETH futures account to net out any residual delta.
• Re-balance when delta/gamma move away from 0 or when the collateral ratio moves away from 2.
• Close out the positions when the IVs converge.

This strategy requires 85-105k in capital when the trade is active. Around 90% of this capital is for the ETH collateral to mint oSQTH at 2x ratio. The rest is for the options and residual futures.

Note: It may be easier to look at relative IVs as a signal to enter/exit Squeeth’s automated crab strategy. Short oSQTH and the delta hedge would be managed by the smart contract and Deribit options could be traded separately.

Technical Description

Below is the strategy in more detail. It assumes we run the strategy independently (not in a portfolio of trades) and does not fully optimize for t-costs. Assume we trade at hourly with time indexed by $t_i$. Further, note that all the Squeeth function calls below are made to the Controller.

Trade-by-trade Breakdown

For each time period $t_1, t_2, \dots$, check if $\frac{\text{EWMA(Squeeth\_IV}_{0:t_{i - 1}})}{\text{EWMA(Option\_IV}_{0:t_{i - 1}})} > \alpha$:

• $\textbf{If YES and we have no active position, open a position}$
  • To go short oSQTH:
    • Compute the # of units of oSQTH to get $50K short exposure given the current price, $\text{oSQTH}_{t_i}$.
    • Compute how much ETH you need to deposit in your vault for a 2x collateral ratio, given $\text{ETH}_{t_i}$ and $\text{normalization\_factor}_{t_i}$.
    • Deposit ETH collateral to mint oSQTH and swap for ETH in Uniswap.
    • To go long options:
      • Identify the strip of OTM puts/calls with expiry closest to and greater than 17.5 days.
      • Filter for the liquid options, removing those with large bid-ask IV spreads and low OI.
      • Size positions across options with $2\Delta K_i$ weights per the replicating portfolio formula.
      • Compute the gamma of the total option portfolio and then scale the total number of lots to match the gamma of the short oSQTH position.
  • If there is any residual delta, put on a ETH futures position to hedge.
• $\textbf{If YES and we have an active position, manage the position:}$
  • If the Deribit options are less than 7 days to expiry, roll the position to the expiry greater than 17.5 days.
  • If the gamma is outside of $[-0.01, 0.01]$, rebalance by buying/selling Deribit options.
  • If the $\text{collateral\_ratio}_{t_i}$ is outside of $[1.75, 2.25]$, add or remove ETH as needed from the Squeeth contract.
  • If the net delta is outside of $[-5, 5]$, use ETH futures position to hedge.
• $\textbf{If NO and we have no active position, there is nothing to do.}$
• $\textbf{If NO and we have an active position, close the position:}$
  • Swap ETH back for oSQTH in Uniswap, burn oSQTH and unlock ETH collateral.
    • Sell the strip of Deribit options.

Backtest

I run a backtest using the Squeeth and Deribit data which approximates the strategy above. The settings are:

• The IV ratio which triggers trades $\alpha = 1.3$.
• T-cost assumptions:
  • ETH futures - Pay 0.1% taker fees on all trades. No price impact.
  • Deribit options - Pay taker fees of $\text{min}( 0.3\% \text{ of ETH price}, 12.5\% \text{ of option price})$ on all trades. Pay 5% in price impact.
  • oSQTH - Pay a total of 1.8% for all trades.
    • Uniswap price impact and pool fees: At current liquidity, swapping $50K of oSQTH for ETH at once costs around 1%. The other way costs 1.6%. I average these to 1.3%.
    • Gas: Looking at the historical distribution of gas costs for oSQTH burn and mint transactions gas costs, I conservatively take another 0.5% on the trade for gas.

Default Settings

Under the default settings, the backtest implies a strategy with annual ER of 125%, vol of 37% and a 3.39 Sharpe. It requires around 100K in capital and generates around 45K in pnl over a 5-month period. Check the bolded results in the sections below to see plots of the returns. Here is what the greeks look like over time:

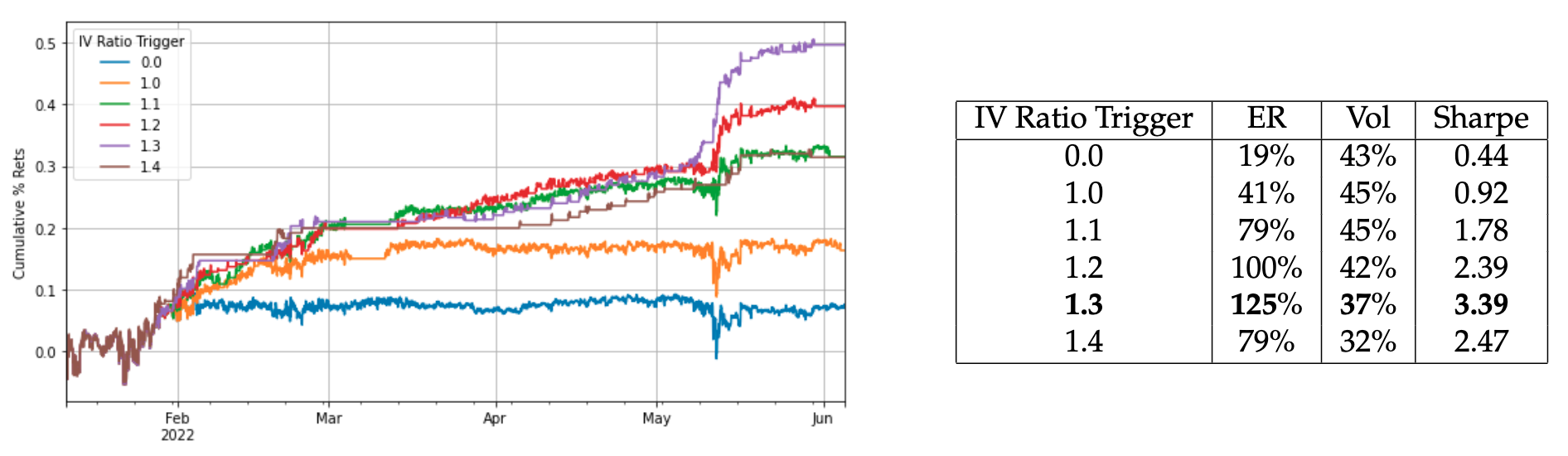
Different IV Ratio Triggers

Here I compare different IV ratio triggers, $\alpha$. Note the 0 case corresponds to being statically short oSQTH and long options independent of the IVs.

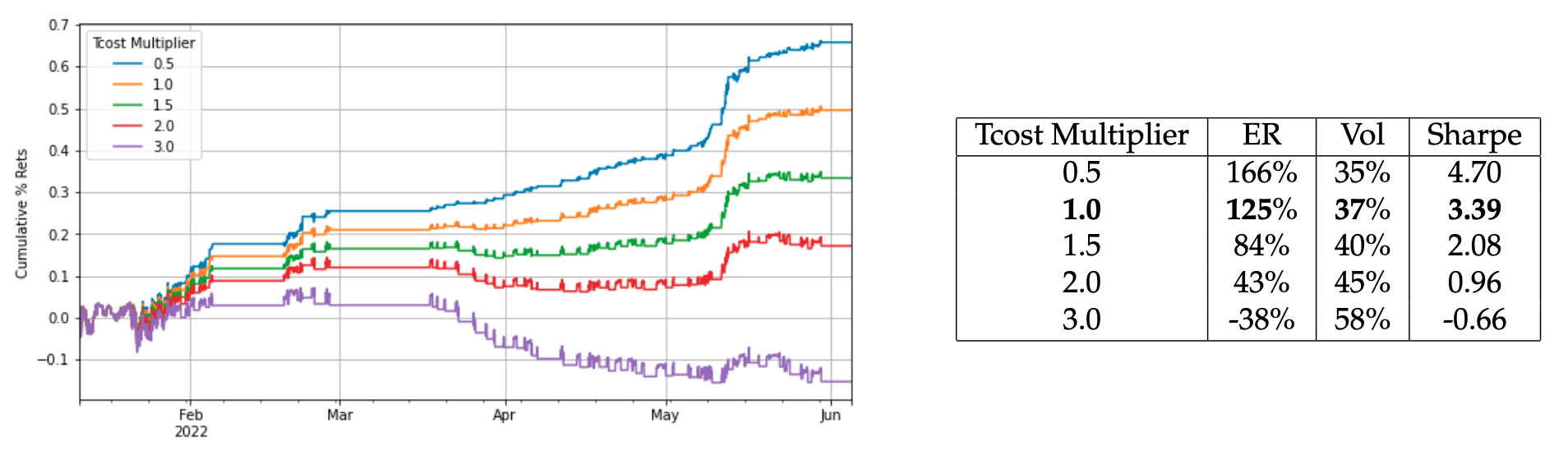
Different T-costs

Here I compare what happens if I multiply the default t-costs, inflating or deflating all of them by a constant factor.

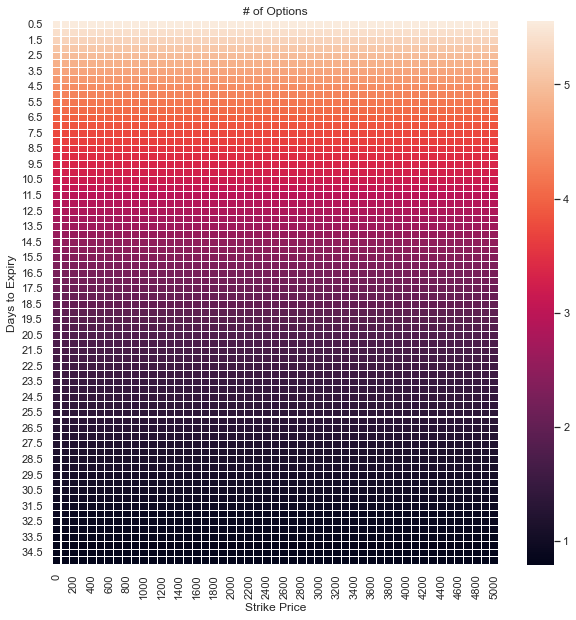
Exact Squeeth Replicating Portfolio

The exact replicating portfolio for Squeeth would be impossible to hold due to rolling costs and liquidity constraints. It requires infinite strikes and expiries.

Recall a power-2 perpetual is a weighted average of power-2 futures expiring at $T_{i} = \frac{P}{N}i$,the times of future funding payments. So, the exact replicating portfolio is a weighted average of the power-2 future replicating portfolios. This requires $2w_iK_0$ of forwards and $2w_{i}dK$ of OTM options across all strikes for each $T_i$, where $w_{i} = \frac{1}{N} \left(\frac{N}{N + 1} \right)^{i}$.

For intuition, consider the case where $P = 17.5$, as in Squeeth, and $N = 35$. The heatmap shows an approximation of the replicating portfolio’s option component. The unit notional weights decay with days to expiry (center of mass = 17.5 days) and are constant across strikes.