Optimization for Deep Learning

This is part 2 of my applied DL notes. I am taking an optimization course this upcoming fall which will cover the more theoretical aspects of optimization and relevance to modern ML. These notes will only convey very high-level intuition of these algorithms and practical advice as relevant to DL. A great supplementary blog post is here.

Overview

Most classical optimization methods are designed for convex optimization. Essentially, all multi-layer NNs with non-linear activations are non-convex in the trainable parameters $(W^{(1)}, \dots, W^{(L)}, b^{(1)}, \dots b^{(L)})$. That is the Hessian $\nabla^{2} L(W, b)$ is neither PSD or NSD everywhere. There are many local minima, many global minima (in the overparameterized case) and saddle points. In high dimensions, the likelihood that at least some eigenvalues at a zero-gradient point are negative and positive is quite high, which makes saddle points more common than local minima. While training NNs is solving a non-convex optimization, many of the intuitions from convex optimization carry over. Importantly, your choice of hyperparameters and algorithm play a much more important role on the solution to which you converge, the speed of convergence and the generalization properties of the solution.

Classical Methods

Gradient Descent

Recall the GD Lemma tells us that for any $L$-smooth function (convex or not), as long as $\eta \leq 1/L$:

$f(x_{t}) \leq f(x_{t - 1}) - \frac{\eta}{2} \| \nabla f(x_{t-1})\|_2^2$

So, using the proper learning rate, as long as we have a non-zero gradient, we can decrease the objective. If $\nabla f(x_{t-1}) = 0$ and $f$ is convex, we are set since $\nabla f(x^{\ast}) = 0 \leftrightarrow x^{\ast} = \arg\min_{x} f(x)$. But in general, GD Lemma only gives convergence in the norm of the gradient. We are guaranteed to find a point such that $\| f(x_t) \|_{2}^2 \leq \epsilon$ in less than:

$T_{\epsilon} = \frac{2(f(x_0) - f(x^{\ast}))}{\eta \epsilon}$

steps. Convergence in actual function value requires convexity, in which case the Mirror Descent Lemma gives the convergence rate:

$f(x_{T}) \leq f(x^{\ast}) + \frac{\|x^{\ast} - x_{0}\|_{2}^2}{\eta T}$

To find a solution with $\epsilon$ accuracy requires $O(1/\epsilon)$ steps. For a strongly convex function this improves to $O(1/\log \epsilon)$.

Second-Order Methods

Consider an example from ZLLS2021 where $f(x_1, x_2) = 0.1x_1^2 + 2x_2^2$. Running GD leads to a solution path as follows:

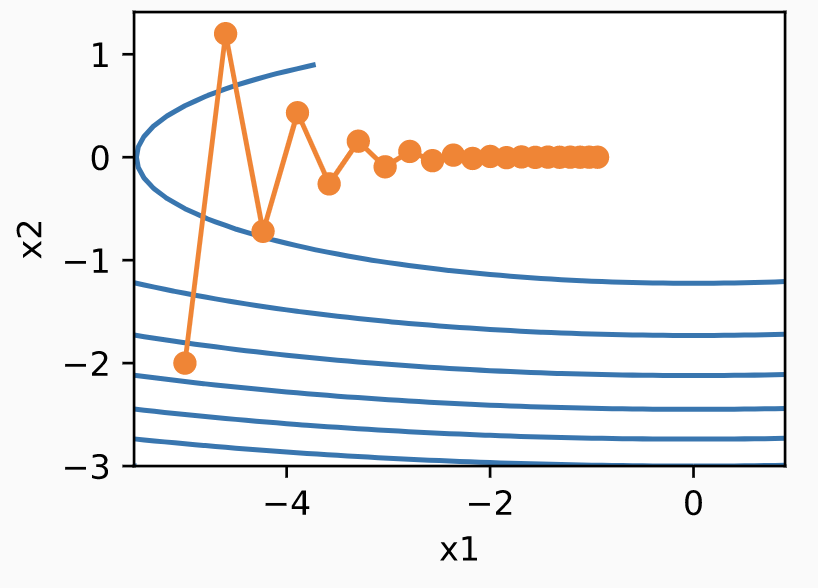
Since the function has a lot more curvature in the $x_2$ direction compared to the $x_1$ direction, the local gradients will zig-zag and only very slowly reach $(0, 0)$. The function $f$ here is 2-smooth, so GD one converges when $\eta \leq 1/2$. Second-order methods attempt to adapt to the local geometry/curvature of a function to handle this issue and get faster convergence rates.

The idea behind Newton’s method is that instead of approximating a function locally with a first-order Taylor expansion (a linear approximation), one uses a second-order Taylor expansion (a quadratic approximation) which yields the optimal update:

$x_{t} \leftarrow x_{t - 1} - \eta \left[\nabla^2 f(x_{t - 1})\right]^{-1} \nabla f(x_{t - 1})$

Intuitively, one can think of this update as scaling the learning rate $\eta$ in different directions depending on the curvature of $f$. Directions with more curvature get scaled down more; directions with less curvature get scaled up. In general, Newton’s method only has a local convergence guarantee. Once you are close enough to $x^{\ast}$ (at step $x^{t_k}$), you get quadratic convergence. Specifically for $t \geq t_k$:

$f(x_t) \leq f(x^{\ast}) + C\left(\frac{1}{2}\right)^{2^{t - t_k + 1}}$

where $C$ depends on the smoothness of $f$ and its gradients. To find a solution with $\epsilon$ accuracy requires O($1/ \log \log \epsilon$) steps. Alternatively, one can see that the number of digits to which the solution $x_{t}$ is accurate for $x^{\ast}$ doubles in each step. For strictly convex functions, global convergence guarantees are possible but only at the $O(1/\log \epsilon)$ rate.

For large-scale ML, second-order methods are infeasible because $\nabla^2 f(x_{t})$ scales quadratically with the number of parameters in your model. Further, inverting such a matrix is can be extremely expensive. A possible solution is to approximate the Hessian with another pre-condition matrix $M$, for example $\text{diag}(\nabla^2 f(x_{t}))$. Additionally, for non-convex problems where the Hessian can have negative values, without any adjustments, Newton’s method may increase the function value.

Line Search

Often GD and Newton’s method are complemented by line search to ensure that each iteration does not overshoot. That is once, $\nabla f(x_{t - 1})$ and $\nabla^2 f(x_{t-1})$ have been computed, one finds an adaptive learning rate $\eta$ which sufficiently decreases $f(x_{t - 1} - \eta \nabla f(x_{t - 1}))$. One can do this in a binary search approach. Again, for large-scale ML this is infeasible because it requires evaluating the objective function of a potentially very large dataset.

SGD

For an ERM problem, our objective function looks like:

$f(x) = \frac{1}{n}\sum_{i = 1} f_{i}(x)$

where $f_{i}(x)$ is the loss on a training point $(x_i, y_i)$. Running GD on this function would require $\Theta(nd)$ computation for parameter dimension $d$. This is infeasible for a large datasets. An alternative is SGD which samples a single point at random to approximate $\nabla f(x_{t})$. Note that assuming iid data, we have $\mathbb{E}[\nabla f_{i}(x_t)] = \nabla f(x_t)$. We have a noisy estimate of the true gradient.

We get the following convergence rate for convex $f$:

$\frac{1}{T} \sum_{t = 0}^{T - 1} \mathbb{E}[f(x_t)] \leq f(x^{\ast}) + \frac{\|x_0 - x^{\ast}\|\sqrt{G}}{\sqrt{T}}$

where $G = \max_{t \in [T]} \mathbb{E}[\| \nabla f_{t} (x_{t})\|_{2}^2]$ and $\eta = \sqrt{\frac{\|x_0 - x^{\ast}\|^2}{GT}}$. Here we see the variance of the stochastic gradient, $G$, plays an important role in the convergence.

The result above relies on sampling with replacement from your training data. However, in expectation, we will only see 67% of the training data. In practice, SGD is run by sampling without replacement but in each epoch the samples are passed through in a different random order.

Mini-Batch SGD

One strategy to reduce the value of $G$ is to use larger batch sizes when using stochastic gradients. That is we use the following updates:

$x_{t} \leftarrow x_{t - 1} - \eta\left(\frac{1}{\lvert \mathcal{B}_t \rvert} \sum_{i \in \mathcal{B}_t} \nabla f_{i}(x_i) \right)$

Say $\lvert \mathcal{B}_t \rvert = \alpha$. Increasing the batch size from 1 to $\alpha$ reduces $G$ by a factor of $\alpha$ (even when sampling with replacement) and hence improves the convergence rate by a factor of $\sqrt{\alpha}$. But per iteration we need to compute $\alpha$ more gradients. There is a statistical-computational tradeoff here which seems to suggest not increasing batch sizes.

However, this perspective ignores the computational advantages due to vectorization and efficient use of cache. The compute cost does not in fact scale linearly with $\alpha$. The simplest example to demonstrate this idea is parallelization across multiple GPUs and servers. If we have 16 servers with 8 GPUs, sending 1 sample to each, we can compute the update for a minibatch of 512 samples in the same time as a single sample. Issues are a bit more subtle when dealing with a single GPU or CPU. A CPU has a small number of registers, than L1, L2 and sometimes L3 cache. These caches increase in size and latency and decrease in bandwith. The key idea is that processors are able to perform many more operations than what the main memory interface can provide it. A 2GHz CPU with 16 cores and AVX-512 vectorization can process upto $2 \times 10^{9} \times 16 \times 32 = 10^{12}$ bytes per second, but a typical processor might have a bandwith of only 100 GB/s. That is one-tenth of what would keep the processor fed. Moreover, not all memory access is created equal. For example, sequential access tends to be faster than first access. The fix here is to avoid loading new data from memory as far as possible and store it locally in CPU cache. With the standard minibatch sizes and vectorized matrix computations, DL libraries can do exactly that. It is useful to set the mini-batch size to a power 2 since that is how computer memory is layed out and accessed.

Accelerated Gradient Methods

The core idea behind accelerated methods is to somehow average the current gradient, $\nabla f(x_t)$, with previous gradients. These methods, much like second-order methods, can adapt to the local curvature of a function. Additionally, they can reduce the variance of stochastic gradients, finding more stable descent directions.

The standard technique is momentum. Let $g_{t}$ denote the standard gradient update (possibly computed by full-batch or minibatch SGD). The simplest implementation would be to use $x_{t} \leftarrow x_{t - 1} - \eta v_{t}$ where $v_{t}$ is defined as:

$v_{t} = \beta v_{t - 1} + g_{t}$

for some $\beta \in (0, 1)$. Expanding $v_{t}$ reveals:

$v_{t} = \beta^{2} v_{t - 2} + \beta g_{t - 1} + g_{t} = \dots = \sum_{i = 0}^{t} \beta^{i} g_{t - i}$

That is our current update, $v_{t}$, amounts to an exponentially-weighted moving average of the standard gradient updates.

Intuitively, momentum increases the effective learning rate in smoother directions of our parameter space and decreases the learning rate in directions with more curvature. For example, consider the ill-conditioned problem shown in the “Second-Order Methods” section. The coordinate of $g_{t}$ associated with $x_{2}$ will be reduced by $\beta v_{t - 1}$ since the signs of updates are switching back and forth. On the other hand, the coordinate of $g_{t}$ associated with $x_{1}$ will increased by $\beta v_{t - 1}$ since the signs of the updates are all in the same direction. Note that $\eta \lim_{t \rightarrow \infty} \sum_{i = 0}^{t} \beta^{i} = \frac{\eta}{1 - \beta}$. Hence, as $\beta \rightarrow 1$, we are effectively using a larger learning rate than permitted by GD along with better behaved descent directions.

A variant of of the usual momentum is more theoretically amenable. For this variant, we have the following result. Assume $f(x_0) = 1$ and $\|x^{\ast} - x_0 \| = 1$. For $\epsilon > 0$, we need at most $\sqrt{\frac{2L}{\epsilon}}$ steps to find $x_{T_{\epsilon}}$ such that $f(x_{T_{\epsilon}}) \leq \epsilon$. GD needs $\frac{2L}{\epsilon}$ to find such a point.

GD vs Momentum in Eigenspace for Quadratic Functions

G2017 have a useful explanation of why momentum works beyond basic intuition. Here we cover one of the most basic results the article conveys. Consider the convex quadratic function:

$h(x) = \frac{1}{2} x^{T}Qx + b^{T}c + b$

For PSD matrices, $Q \succ 0$, the minimizer is $x^{\ast} = -Q^{-1}c$ and $h(x^{\ast}) = b - \frac{1}{2}c^{T}Q^{-1}c$. Then, we can write $h(x)$ as follows:

$h(x) = \frac{1}{2}(x - Q^{-1}c)^{T}Q(x - Q^{-1}c) + b - \frac{1}{2}c^{T}Q^{-1}c$

The gradient $\nabla h(x) = Q(x - Q^{-1}c)$. Now consider the eigendecomposition of $Q = O^{T} \Delta O$ and change of variables $z = O(x - Q^{-1}c)$. That is $z$ is the distance to the minimizer represented with respect to the eigenvectors of $Q$. Now, we have:

$h(z) = \frac{1}{2}z^{T}\Delta z + b^{'}$

where $b^{'} = b - \frac{1}{2}c^{T}Q^{-1}c$. Now, we have GD gives:

$z_{t} = z_{t - 1} - \eta \Delta z_{t - 1} = (I - \eta\Delta) z_{t - 1} = (I - \eta \Delta)^{t} z_0$

Hence GD does not mix between eigenspaces. In the original space, we have:

$x_{t} - x^{\ast} = O^{T}z_{t} = O^{T}(I - \eta \Delta)^{t} z_0$

Here we see that the optimization proceeds in a coordinate-wise manner with respect to the eigenvectors of $Q$. Each element of $z_0$ is the component of the error in the initial guess with respect to the eigenbasis $O$. Each such component independently follows a path to the minimum, decreasing at a exponential rate of $1 - \eta \lambda_i$. So, convergence in the directions of the large and small eigenvectors occurs fast and slow, respectively. In order to converge, we need $\lvert 1 - \eta \lambda_i \rvert < 1$ for all $i$. All valid $\eta$ must obey:

$0 < \eta \lambda_i < 2$

The overall convergence rate is determined by:

$\text{rate}(\eta) = \max_{i} \lvert 1 - \eta \lambda_i \rvert = \max \{\lvert 1 - \eta \lambda_1 \rvert, \lvert 1 - \eta \lambda_d \rvert\}$

This rate is minimized when the rates for $\lambda_1$ and $\lambda_d$ are the same, which gives an optimal $\eta = \frac{2}{\lambda_1 + \lambda_d}$ and an optimal rate:

$\frac{\lambda_d/\lambda_1 - 1}{\lambda_d/\lambda_1 + 1}$

Hence the convergence rate is determined by the condition number of $Q$.

A similar analysis for momentum reveals:

$\begin{aligned} v_{t} &= \beta v_{t - 1} + \Delta z_{t - 1}\\ z_{t} &= z_{t - 1} - \eta v_{t} = (I - \eta \Delta)z_{t - 1} - \eta \beta v_{t - 1} \end{aligned}$

We can write this update in a component-wise fashion with the following:

$\begin{bmatrix} v_{t + 1}^{i} \\ z_{t + 1}^{i} \end{bmatrix} = \begin{bmatrix} \beta & \lambda_i \\ -\eta \beta & (1 - \eta \lambda) \\ \end{bmatrix} \begin{bmatrix} v_{t}^{i} \\ z_{t}^{i} \end{bmatrix} = R(\beta, \lambda_i, \eta) \begin{bmatrix} v_{t}^{i} \\ z_{t}^{i} \end{bmatrix} = R(\beta, \lambda_i, \eta)^{t} \begin{bmatrix} v_{0}^{i} \\ z_{0}^{i} \end{bmatrix}$

With some linear algebraic tricks, one can write $R^{t}$ in terms of its eigenvalues, $\sigma_1$ and $\sigma_2$. This analysis shows that the rate of convergence is determined by $\min\{\sigma_1, \sigma_2\}$. Valid values for $\eta$ and $\beta \in [0, 1]$ obey:

$0 < \eta \lambda_i < 2 + 2\beta$

Here we see that momentum allows us to increase the learning rate by a factor of 2 compared to GD before diverging.

AdaGrad

Imagine a very large scale NLP model. A common problem is sparse features. It is clear that some words occur very frequently while others are rare. If we use a fixed learning rate schedule with a $O\left(\frac{1}{\sqrt{t}}\right)$ rate, we will see many more parameter updates for frequent features, while convergence for infrequent features will lag behind. AdaGrad addresses these issues by using a learning rate of the form $\eta_{i} = \frac{\eta_0}{\sqrt{s(i, t) + c}}$ where $s(i, t) = s(i, t - 1) + (\nabla f(x))_{i}^{2}$. Coordinates with consistently large gradients are scaled down a lot, while coordinates with small gradients are scaled up.

The benefits of AdaGrad are best understood in context of approximate second-order methods and pre-conditioning. Recall from the discussion above on GD in eigenspace, that the convergence rate is driven by $\frac{\lambda_d}{\lambda_1}$. For the convex quadratic problem, we could in theory improve the convergence rate by a change of basis $y = \Delta^{-1/2}Ox$. But this modification requires computing the eigenvectors and eigenvalues, which is much more expensive than solving the original problem itself. Another solution would be use $y = \text{diag}(Q)^{-1/2}x$. In this case, we have $\tilde{Q} = \text{diag}(Q)^{-1/2}Q\text{diag}(Q)^{-1/2}$ and $\tilde{Q}_{ii} = 1$. In practice, this improves the condition number considerably.

The solutions above do not work for DL because we typically do not have access to the Hessian of the objective function and computing it for a given $x$ requires $O(d^{2})$ time and space to compute, which is infeasible. AdaGrad approximates the diagonal of the Hessian by using the magnitude of the gradient itself. Recall for the convex quadratic objective we have $\nabla h(z) = \Delta z$. So, the gradient depends on $\Delta$ and $z$, which measures distance from optimality. If $z$ were fixed as a function of $x$, then that is all we need. With SGD, we will see non-zero gradients even at the optimum. So, AdaGrad uses their variance as a proxy for the scale of the Hessian.

In practice, the AdaGrad updates look as follows:

$\begin{aligned} g_{t} &= \nabla_{w} l(y_{t}, f(x_{t}, w))\\ s_{t} &= s_{t - 1} + g_{t}^{2}\\ w_{t} &= w_{t - 1} - \frac{\eta}{\sqrt{s_{t} + \epsilon}} g_{t} \end{aligned}$

All these updates are done coordinate-wise. The $\epsilon$ is a small number to avoid divide by zero errors. Since $s_{t}$ grows at a linear rate, we see that AdaGrad corresponds to a $O\left(\frac{1}{\sqrt{t}}\right)$ rate on a per-coordinate basis. An issue in DL is that this schedule might decrease the learning rate too aggressively. The variants below address this problem.

RMSProp

Note that $s_{t}$ is unbounded and grows at a linear rate. RMSProp attempts to decouple learning rate scheduling from coordinate-wise adaptive rates. The idea is to normalize $s_{t}$. Just like momentum, one way to do normalize $s_{t}$ is with leaky averages:

$\begin{aligned} s_{t} &= \gamma s_{t - 1} + (1 - \gamma) g_{t}^{2}\\ x_{t} &= x_{t - 1} - \frac{\eta}{\sqrt{s_{t} + \epsilon}}g_{t} \end{aligned}$

The above formulation allows to control the learning rate schedule $\eta$ independently of the per-coordinate basis scaling. Note that we have:

$s_{t} = (1 - \gamma)(g_{t}^2 + \gamma g_{t - 1}^2 + \gamma^{2}g_{t - 2}^2 + \dots)$

Since $1 + \gamma + \gamma^{2} + \dots = \frac{1}{1 - \gamma}$, the sum of the weights is normalized to 1. In practice, $\gamma \approx 0.9$ and $\eta \approx 0.001$.

AdaDelta

AdaDelta is another modification of AdaGrad which eliminates the need for an initial learning rate $\eta$ all together. Intuitively, updates to parameters should be in the units of the parameter. For example, if a parameter represents years, updates should also be in units of years. However, this is not the case for many of the algorithms above. For example, for GD and momentum, we have:

$x_{t} - x_{t - 1} \propto \nabla f(x_{t - 1}) \propto \frac{1}{\text{units of } x}$

In AdaGrad, the update is unitless. Newton’s method gets this right. We have:

$x_{t} - x_{t - 1} \propto \left[\nabla^2 f(x_{t - 1})\right]^{-1} \nabla f(x_{t - 1}) \propto \text{units of } x$

AdaDelta uses a rescaled gradient which similarly has the correct units. To do so, we keep track of both a leaky average of second moment of the gradient like RMSProp as well as a leaky average of the second moment of the changes in the parameters themselves:

$\begin{aligned} s_{t} &= \rho s_{t - 1} + (1 - \rho) g_{t}^2\\ \Delta x_{t} &= \rho \Delta x_{t - 1} + (1 - \rho)(g_{t}^{\ast})^{2} \end{aligned}$

where $g_{t}^{\ast}$ is the rescaled gradient:

$g_{t}^{\ast} = \frac{\sqrt{\Delta x_{t - 1} + \epsilon}}{\sqrt{s_t + \epsilon}} \odot g_{t}$

So, AdaDelta can be viewed as attempting to approximate Newton’s method or automating the choice of $\eta$.

The update we use is $x_{t} = x_{t - 1} - g_{t}^{\ast}$.

Adam

Adam combines many of the merits of mini-batch SGD, momentum and RMSProp into one algorithm. It is one of the go-to optimization techniques in DL today, but does not have any convergence guarantees (even for convex problems. In practice, Adam works well for training NNs.

Adam keeps track of two EWMAs: one for momentum and one for the second moment of the gradient:

$\begin{aligned} v_{t} &\leftarrow \beta_{1} v_{t - 1} + (1 - \beta_{1}) g_{t}\\ s_{t} &\leftarrow \beta_{2} s_{t - 1} + (1 - \beta_{2}) g_{t}^2 \end{aligned}$

Common choices are $\beta_{1} = 0.9$ and $\beta_{2} = 0.999$, so the variance term moves much slower than the momentum term. Initializing $v_0 = s_0 = 0$ creates significant bias towards small values. Using $\sum_{i = 0}^{t} \beta^{i} = \frac{1 - \beta^{t}}{1 - \beta}$, we can normalize the state variables as:

$\hat{v}_{t} = \frac{v_{t}}{1 - \beta_1^{t}} \quad \quad \text{and} \quad \quad \hat{s}_{t} = \frac{s_{t}}{1 - \beta_2^{t}}$

The update equations are:

$\begin{aligned} g_{t}^{'} &= \frac{\eta \hat{v}_t}{\sqrt{\hat{s}_t} + \epsilon}\\ x_{t} &\leftarrow x_{t - 1} - g_{t}^{'} \end{aligned}$

These are similar to RMSProp, but with two differences. First, one uses momentum instead of the usual gradient. Second, there is a minor re-formulation of the denominator, which works slightly better in practice. Typically, $\epsilon = 10^{-6}$.

In summary, Adam takes advantage of momentum and scale (per the state variables) to get faster, more stable convergence. There is a de-biasing component to handle the initialization and EWMA. Finally, per RMSProp, the learning rate is de-coupled from the coordinate-wise scaling.

Yogi

Adam can diverge when the second moment estimate in $s_{t}$ blows up. We can re-write the Adam update as:

$s_{t} \leftarrow s_{t - 1} + (1 - \beta_{2})(g_{t}^2 - s_{t -1})$

If $g_{t}^2$ has high variance or updates are sparse, then $s_{t}$ may forget the past quickly. Yogi proposes the following update instead:

$s_{t} \leftarrow s_{t - 1} + (1 - \beta_{2})g_{t}^2 \odot \text{sgn}(g_{t}^2 - s_{t -1})$

Note here the magnitude of the update no longer depends on the size of the deviation. In Adam, when $s_{t - 1}$ is much larger than $g_{t}^{2}$, the effective learning rate increases rapidly. In Yogi, when $s_{t - 1}$ is larger than $g_{t}^2$, the effectively learning rate also increases, but in a much more controlled fashion.

Dynamic Learning Rates

Learning rate scheduling is more important for non-convex problems compared to convex problems. Some considerations here are:

• Recall the magnitude of the optimal learning rate is to some degree determined by the “condition number” of the problem.

• When using stochastic methods like SGD or minibatch SGD, dynamic learning rates become important. Even when one is close to the optimum, noise in the gradient can make it difficult to converge. Setting the learning rate too large and you will overshoot the optimum. On the other hand, setting the learning rate too small can stall convergence earlier in the process. For convex problems, we typically set a schedule at a $O(t^{-1/2})$ rate, but for DL, we may want to decay faster.

• Warmup: Large steps at the beginning may not be useful because we use random initialization.

• Generalization: There is some theoretical backing supporting the idea that small step sizes improve generalization by preventing memorization in DL tasks.

While many of the algorithms we considered above (momentum, AdaGrad, etc.) do some form of adaptive learning rate adjustment, they typically still require a learning rate schedule and this additional lever can be important to get good test performance.

Some common strategies for adjusting $\eta$ are as follows:

$\begin{aligned} \eta(t) &= \eta_i \quad \text{if} \quad t_i \leq t \leq t_{i + 1}\\ \eta(t) &= \eta_0 e^{-\lambda t}\\ \eta(t) &= \eta_0 (\beta t + 1)^{-\alpha}\\ \eta(t) &= \eta_{T} + \frac{\eta_0 - \eta_T}{2}\left(1 + \cos\frac{\pi t}{T}\right) \end{aligned}$

In the first scenario, the learning rate is decreased whenever optimization stalls in a piece-wise constant fashion. That is once we reach a stationary point in terms of the distribution of the weight vectors, we decrease the learning rate to obtain a higher quality proxy to the a good local minimum. This is common in DL. The exponential and polynomial schedules are natural choices with theoretical guarantees for convex problems. The last policy is the cosine scheduler. Here $\eta_{T}$ is a target rate for time $T$. The idea is that we may not want to decrease the learning rate too much in the beginning and may want to refine the solution in the end using a very small learning rate. For $t > T$, the learning rate is simply pinned to $\eta_T$.

For complicated architectures, warmup is an important concept. Taking large steps early can be problematic since random initialization can cause the algorithm to diverge early for those parts of the network that aare the most difficult to optimize. Instead, one can linearly increase from a learning rate of 0 to the initial maximum in a number of “warmup” steps before implementing the desired policy.

Optimization Checks

Gradient Checking

In most cases, you will rely on your DL framework’s built in autodiff functionality to do backprop. There are some exceptions where you may implement your own backward function. For example, if you have a function that cannot be expressed as composition of other differentiable functions or if you have a shortcut to speed-up a particularly complicated chain rule.

Gradient checking ensures your backprop calculation is correct. You comapre the analytic gradient to the numerical gradient. Some tricks to make sure you are doing this robustly:

First, use the centered formula: $\frac{\partial f(x)}{\partial x} = \frac{f(x + h) - f(x - h)}{2h}$ where $h$ is a small number such as $10^{-5}$. This is a better gradient approximation than the usual formula because it is a second-order approximation and has error on the order of $O(h^2)$ instead of $O(h)$.

Second, use the relative error for comparison:

$\frac{\lvert f_{a}^{'} - f_{n}^{'}\rvert}{\max\left(\lvert f_{a}^{'} \rvert, \lvert f_{n}^{'} \rvert \right)}$

If the relative error is less than $10^{-7}$, you are probably okay. Else, there may be something wrong. Also, note the relative errors will tend to increase for larger/deeper NNs.

Third, sometimes a gradient check might fail even though it is correct due to issues with numerical precision. To prevent this, use double instead of single precision floating point numbers. Also, stick around the active range of floating point. That is your loss on a minibatch is tiny (less than $10^{-10}$), then it may make sense to scale up your loss function by a constant to a nicer range where floats are more dense. Finally, be careful with $h$. Too small a $h$ can run into issues due to cancellation.

Fourth, kinks in your objective can cause issues with gradient checks. Consider gradient checking the ReLU function at $x = -10^{-6}$. It will have a gradient of zero, but if $h > 10^{-6}$, then $f(x + h)$ will introduce a non-zero contribution to your numerical approximation. One solution here is to only use a few datapoints since the loss function will contain less kinks and you are less likely to cross a threshold doing the numerical approximation. This also speeds up your gradient checking process.

Fifth, do gradient check during a “characteristic” mode of operation. A gradient check can succeeed at a particular random point in parameter space even if the gradients are not implemented properly globally. This can be due to pathological edge cases caused by small initializations near 0. It is good to train your model for a while and let the loss decrease in a burn-in period. From then, you can run the gradient checking process.

Sixth, if you include weight decay the regularization loss can overwhelm the data loss. This can make it look like your gradient checks are passing because of the regularization term (with the more easily computable gradient) is correct, even though your data loss terms are incorrect. A solution would be to turn off regularization and run the checks. Then, independently check the gradients due to the regularization loss.

Seventh, turn off non-deterministic effects in the network such as dropout or random data augmentations. Otherwise, this can introduce huge errors in the numerical gradient. But in that case you are also not checking these features (i.e., dropout may not be backpropogated correctly). A better solution might be to force a particular random seed before evaluting $f(x + h)$, $f(x - h)$ and the analytic gradient.

Other Sanity Checks

In addition to gradient checking, it is a good idea to run a few more general sanity checks before trying an expensive optimization.

First, often given the number of classes in your dataset, the fraction of points in those classes and your loss function you can calculate the loss on a model initialized with zero weights. Make sure you see the actual loss matches up. For example, for CIFAR-10 softmax classification the initial should be 2.302, because there are 10 classes each with fraction around 0.1 and $-\ln(0.1) = 2.302$.

Second, increasing regularization should increase your training loss.

Third, overfit a tiny subset of the data. Use 20 samples from your training data and make sure you can get to zero loss. It is possible you pass this check, but the NN is still incorrectly implemented.